Mathematik
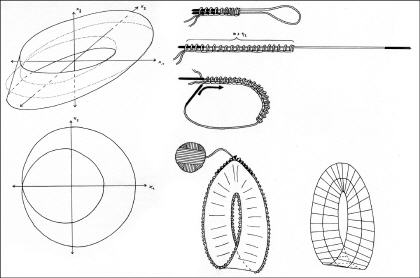
Ein gestricktes Möbiusband
Aus meiner Studienzeit:
Während meines Studiums (1978-1984) war es üblich, dass einige Studentinnen während der Vorlesung ihr Strickzeug auspackten und zu stricken begannen. Ein Mathematik-Professor meinte, sie könnten ihm doch mal ein Möbiusband stricken. Er würde dies besonders würdigen.
|
Nach einiger Zeit bekam er eins geschenkt - von mir. Er war voll begeistert und wir haben uns lange darüber unterhalten.
Ganz nebenbei hatte ich anschaulich gezeigt, dass das Möbiusband ein Faserbündel über dem S1 ist.
|
Eine Rechenhilfe für meine Kinder
Ich habe während der Grundschulzeit für meine Kinder Napier-Stäbe gebastelt, sozusagen den ersten „Taschenrechner“.

|
|
Mit Hilfe von Napier-Stäben kann man leicht und übersichtlich multiplizieren und dividieren.
Die Stäbe unterstützen gleichzeitig das Lernen der Multiplikationsreihen des kleinen 1x1.
Hier die Beschreibung der Napier-Stäbe und der Umgang mit ihnen.
Download [1.696 KB]
als ppsx
|
Das Bild rechts zeigt meine selbst gebastelten Napier Stäbe für meine Kinder zur Nutzung während der Grundschulzeit.
Die Stäbe haben einen Kern aus Holz mit einem Querschnitt von 15mm im Quadrat.
Hier die Bastelvorlage für die Napier-Stäbe.
Download [25 KB]
als pdf
|
|

|
Meine Taschenrechner-Sammlung
Ich interessiere mich für mechanische und elektronische Rechenhilfen. Im Laufe der Zeit ist da einiges zusammengekommen.
Einige Rechner muss man vermutlich kurz vorstellen.
Es ist schon faszinierend, welche Rechenoperationen mit diesen Geräten durchführbar sind. Der Mensch hat wohl schon immer versucht, formale mechanische Rechenoperationen durch Hilfsmittel zu vereinfachen. Selbstverständlich hat auch hier alles seine Zeit, Materialien und Materialbearbeitung müssen zur Verfügung stehen. Viele Apparate wurden im Vorfeld nur theoretisch beschrieben, scheiterten jedoch dann vorerst an der technischen Ausführbarkeit.

|
|

|
|

|
Der Abakus
Hier ein Chinesischer Suanpan.
Die einfachere Variante habe ich noch in der Schule als ein Rahmen mit 10x10 farbigen Kugeln kennen gelernt.
Beim traditionellen Abakus werden 1-wertige (untere) und 5-wertige (obere Reihe) Steine verwendet
|
|
Der Addiator
Ein mechanisches Gerät bei dem man mit Hilfe eines bleistiftähnlichen Stabes Zahlenreihen nach unten ziehen oder nach oben schieben muss, je nachdem, ob sich ein Übertrag ergibt oder nicht.
Auf der Vorderseite wird addiert. Auf Rückseite kann subtrahiert werden.
Der Speicher wird „resetted“ indem man an dem Bügel oben zieht.
|
|
Der Rechenschieber
Ein unentbehrliches Gerät für Techniker vor Erfindung des Taschenrechners.
Die Idee: Der Logrithmus ist ein Homomorphismus
ln:(R+,*)->(R,+)
vermöge der Operation
ln(a*b)=ln(a)+ln(b)
Produkte können also über Summen und diese über Addition (Aneinanderlegen) von Strecken abgebildet werden.
Kann man also intuitiv bedienen, auch ohne wirklich zu wissen, was ein Logarithmus ist.
Habe ich in der Schule gerade so verpasst, weil/als die ersten Taschenrechner eingeführt wurden. Die Bedienung musste ich mir also selbst aneignen.
|

|
|

|
|

|
Otis King Rechenstab
Der Rechnstab ist weniger bekannt, er ist eigentlich eine Abwandlung des Rechnschiebers.
Die logarithmische Skala ist hier um einen Stab gewickelt.
Das Gerät sieht ein bisschen aus wie ein Teleskopfernrohr.
|
|
Die Curta
Mein Liebling unter den Rechengeräten.
Groß wie ein Kaffeebecher, wirkt die Curta mit der Kurbel am oberen Ende wie eine alte Kaffeemühle.
Durch die ausgeklügelte Technik beherrscht sie die vier Grundrechenarten und das Wurzelziehen.
|
|
Mechnischer Tischrechner
Etwas schwerer als die anderen Geräte, mehr im Kilogramm-Bereich, also kein Taschenrechner mehr.
Die Werte werden über Reiter eingestellt, gerechnet wird mit Hilfe der seitlich angebrachten Kurbel.
Von der Idee her ist das Gerät der größere Verwandte der Curta.
|

|
|

|
|

|
HP41CV
Habe ich mir während des Studiums um 1980 gekauft für ca. 1000,00 DM (heutige Kaufkraft: 1200,00 EUR), dafür aber mit allem pi-pa-po: Alphanumerische Tastatur und Display, programmierbar, UPN-Logik, externer Magnetkartenleser.
|
|
HP-12C
Bis heute verwende ich lieberTaschenrechner mit UPN-Logik: „umgekehrt polnische Notation“.
Durch Verwendung eines rollierenden Speichers (Stapel)
wird aus
5*3=
die Rechenoperation
5-enter-3-mal.
Durch geschicktes Einsetzen dieser Funktion kann man sich damit Klammersetzungen bei größeren Rechenoperationen ersparen.
Aus
5*(3+4)=
wird
5-enter-3-enter-4-plus-mal.
|
|
HP 35S
Meine neueste Anschaffung.
Ein wissenschaftlicher Rechner
Auf den ersten Blick gleicht er dem HP41CV, kann aber deutlich mehr.
Auch hier fällt sofort die große ENTER-Taste auf.
|
Letzte Änderung am 18. Jan. 2025